12時間目：単利と複利を学ぼう

こんにちは。

けいです。

今日は金利が発生する際の単利と複利について学んでいきましょう。

単利と複利

まず最初に、金利とはお金を貸す対価として借りた側より受け取れる金額を割合で表したものでした。

そして金利は基本的に1年間預けた場合の年利として表記をされ、利息の計算は元金×利息×預入日数で算出をされました。

そしていざ利息が付与される際には単利であるか複利であるかが大きなポイントとなります。

単利とは当初の元本にのみ利息が発生する運用の方法です。

当初の金額を基にして毎年計算されるため、元本が変わらなければ受け取れる利息も毎年同じ金額となります。

一方で複利とは付与された利息に対しても利息計上がされるようになるため、受け取れる利息は時間を追うごとに雪だるま式に増えるようになります。

以下の図は1万円をスタートとした時に年利2%で単利と複利それぞれの増え方を表したものになります。

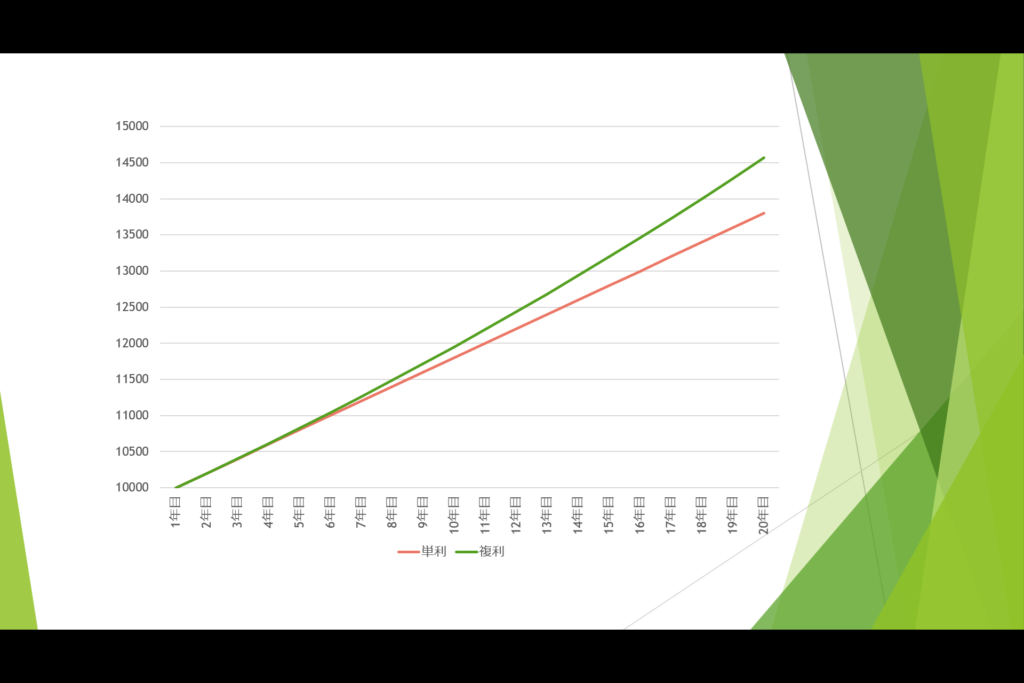
最初は大きな違いではありませんが、時間を追うごとにその差が広がっていることがわかりますね。

20年後にはおよそ700円ほどの差が生まれています。

元金に対して7%の違いとなるためバカにできないでしょう。

続けて年利4%の動きもご確認ください。

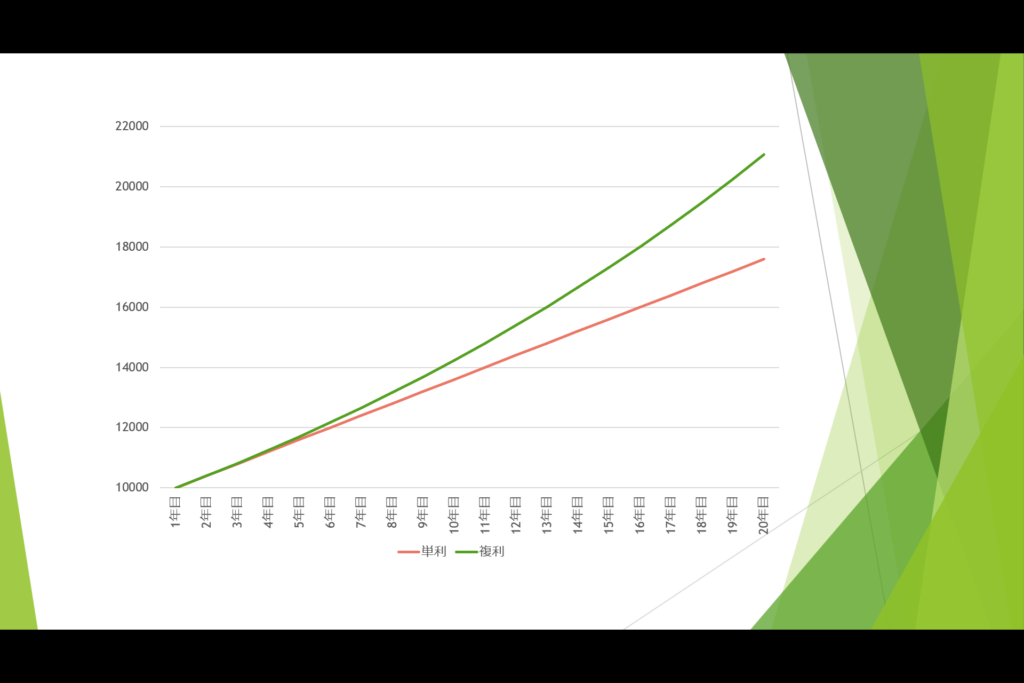
先ほどの図に比べて差の広がり方が顕著になっており、20年後における違いは3500円にもなりました。

割合でみると35%の違いとなります。

雪だるま式に増えていく複利では利率が高い期間が長いほど効果が大きくなっていきます。

これが複利の魔法とも言われる働きですね。

72の法則

みなさんは72の法則といったものを聞いたことがあるでしょうか？

これは複利運用で資金を2倍にするためにかかる期間を計算できる法則となります。

考え方は簡単で、72を金利で割るだけです。

例えば金利が2%だった場合、72÷2%=36年となるため、2%の金利で元金を倍にするためには36年必要であるという事になります。

もし金利が4%だった場合は72÷4%=18年で2倍になるという事ですね。

ちなみに単利4%で元金を2倍にするには25年かかるので、複利の力がいかに大きいかが実感できるかと思います。

またこの式を応用することで、元金を2倍に増やすためにどれくらいの期間が必要かを計算することも可能です。

その場合は72を目標とする期間で割るだけで計算ができます。

例えば10年で元金を2倍にしたいのであれば72÷10年=7.2%の金利が必要であるということがわかります。

7.2%ものリターンを期待する場合は相応のリスクが生じますから、ここからもリスクとリターンは切れない関係であることがわかりますね。

まとめ

今日は単利と複利について学んでいきました。

例えば定期預金ひとつ取っても定期の種類や預入期間によって異なってくるため、預入時はしっかりと確認していきましょう。